Rebecca Writes: Don't Hate Me Because I'm Irrational!

Most rational people turn tail and run when they hear the term irrational numbers. They figure if they can't understand the rational numbers, how are they going to understand those crazy numbers that fly off the handle at the slightest provocation. But there's no reason to be on tenterhooks while in the presence of an irrational number. While it is true that irrational numbers are a tad difficult to pin down, the term irrational when applied to numbers has nothing to do with their unreasonableness, but rather, it tells us that these are numbers that can't be represented as a ratio of two integers.

We've known about rational numbers almost as long as we've known that the sum of the squares of the sides of a right triangle is equal to the square of the hypotenuse, which you probably recognize as the pythagorean theorem. (And I'm using the word we in the last sentence to refer to humanity collectively, so that means around 2500 years ago, since the time of the Pythagoreans, rather than since the time you were in 5th grade.)

The story of the discovery of rational numbers goes something like this: Mr. Pythagoras loved numbers. He loved numbers a whole lot. He loved them because he thought they were beautiful and perfect and pure and tidy, so perfect and pure and tidy that every single number could be represented as a ratio of two whole numbers. So perfect that the sum of the squares of the sides of a right triangle was exactly equal to the square of the hypotenuse. And isn't that just the nicest, tidiest thing you've ever heard?

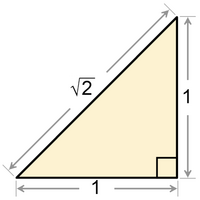
Unfortunately, Pythagorus had a smart aleck student who began fooling around with the pythagorean theorum, starting, as was the perfectly rational thing to do, with a right triangle with sides of one unit, just like the one in the picture above. After a bit of calculation, he discovered--ta da!--that the hypotenuse was exactly √2 units in length. And as any good student of Pythagorus would do, he decided to put √2 in the form of a ratio of two whole numbers.

He worked things out something like this:

√2 = m/n, in which m/n is a fraction in lowest terms.

This much was assumed by definition, since the Pythagoreans assumed that all numbers could be expressed by a ratio of two whole numbers. Next, he squared both sides, and came up with this:

2 = m²/n²

Then he multiplied both sides by n² (and reversed sides) and got:

m² = 2n²

This told him that m must be a multiple of 2, because we know that the square of an even number is even, and since 2n² is even, m must be even. This means we can substitue 2q in the equation for m, since m is a multiple of 2:

4q² = 2n²

And then he divided both sides by 2:

2q² = n²

Which showed him that n must be a multiple of 2 as well. (See the reasoning regarding squares of even numbers above.)

And therein lies the rub. Remember, the student started out with the assumption that that m/n was a fraction in lowest terms. If both m and n are multiples of two, then m/n can't be a fraction in lowest terms, so there's no way to represent √2 as a fraction in lowest terms. Meaning, of course, that √2 is not a rational number, but an irrational one.

Now let's leave the math behind and get back to the story. Mr. Pythagorus's student did what any student would do. He said, "Hey Teach! Look at this!" Unfortunately for the student, his proof undermined the entire belief system of his famous teacher, and as the story goes, Pythagorus did what any perfectly rational person would do, he had the student executed rather than take the chance the secret of irrational numbers would get out to the rest of the world. He also insisted that the rest of the class take an oath of secrecy, with the threat of death for any tattletale.

If I were you, I'd be a little sceptical of this story, since there are about a million different versions of it floating around, proving that mathematicians can embellish with the best of them. What we do know for sure is this: The Pythagoreans discovered irrational numbers*, and they used the proof given above to prove that √2 was irrational. That means their confidential info leaked out anyway, proving that mathematicians can't keep a secret, either.

*Although the Egyptians may have beaten them to the punch.

Sources